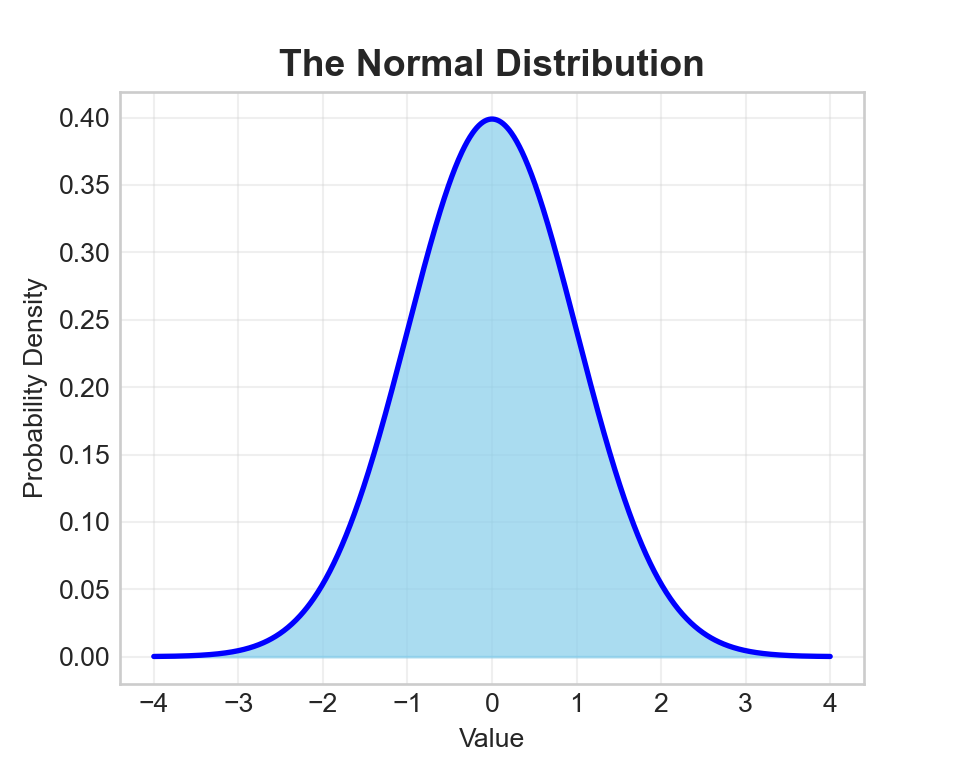
Normal Distributions and the Central Limit Theorem

Sam Kamperis

Wednesday, July 16, 2025

Introduction

Today we explore the beauty of normal distributions and one of statistics’ most important theorems.

Learning Outcomes

By the end of this session, you will be able to:

• Understand what a normal distribution is and its key properties
• Recognize the parameters μ (mean) and σ (standard deviation) that define a normal distribution
  
• Visualize normal distributions with different parameters using Python
• Understand the empirical rule (68-95-99.7 rule)
• Comprehend the Central Limit Theorem and its significance
• Demonstrate the CLT through Python simulations with various distributions
• Apply knowledge of normal distributions to real-world scenarios

What is a Normal Distribution?

The normal distribution (also called the Gaussian distribution) is a continuous probability distribution that:

• Has a characteristic bell-shaped curve
• Is symmetric around its mean (μ)
• Is completely defined by two parameters: mean (μ) and standard deviation (σ)
• Appears frequently in nature and statistics

Mathematical formula:

\[f(x) = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2}\]

Where: - μ = mean (center of distribution) - σ = standard deviation (spread of distribution) - π ≈ 3.14159… - e ≈ 2.71828…

Visualizing Normal Distributions

# Create different normal distributions
x = np.linspace(-8, 8, 1000)

# Different means, same standard deviation
y1 = norm.pdf(x, loc=0, scale=1)    # μ=0, σ=1
y2 = norm.pdf(x, loc=2, scale=1)    # μ=2, σ=1
y3 = norm.pdf(x, loc=-2, scale=1)   # μ=-2, σ=1

plt.figure(figsize=(10, 6))
plt.plot(x, y1, 'b-', linewidth=2, label='μ=0, σ=1')
plt.plot(x, y2, 'r-', linewidth=2, label='μ=2, σ=1')
plt.plot(x, y3, 'g-', linewidth=2, label='μ=-2, σ=1')

plt.title('Normal Distributions with Different Means', fontsize=14, fontweight='bold')
plt.xlabel('Value')
plt.ylabel('Probability Density')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()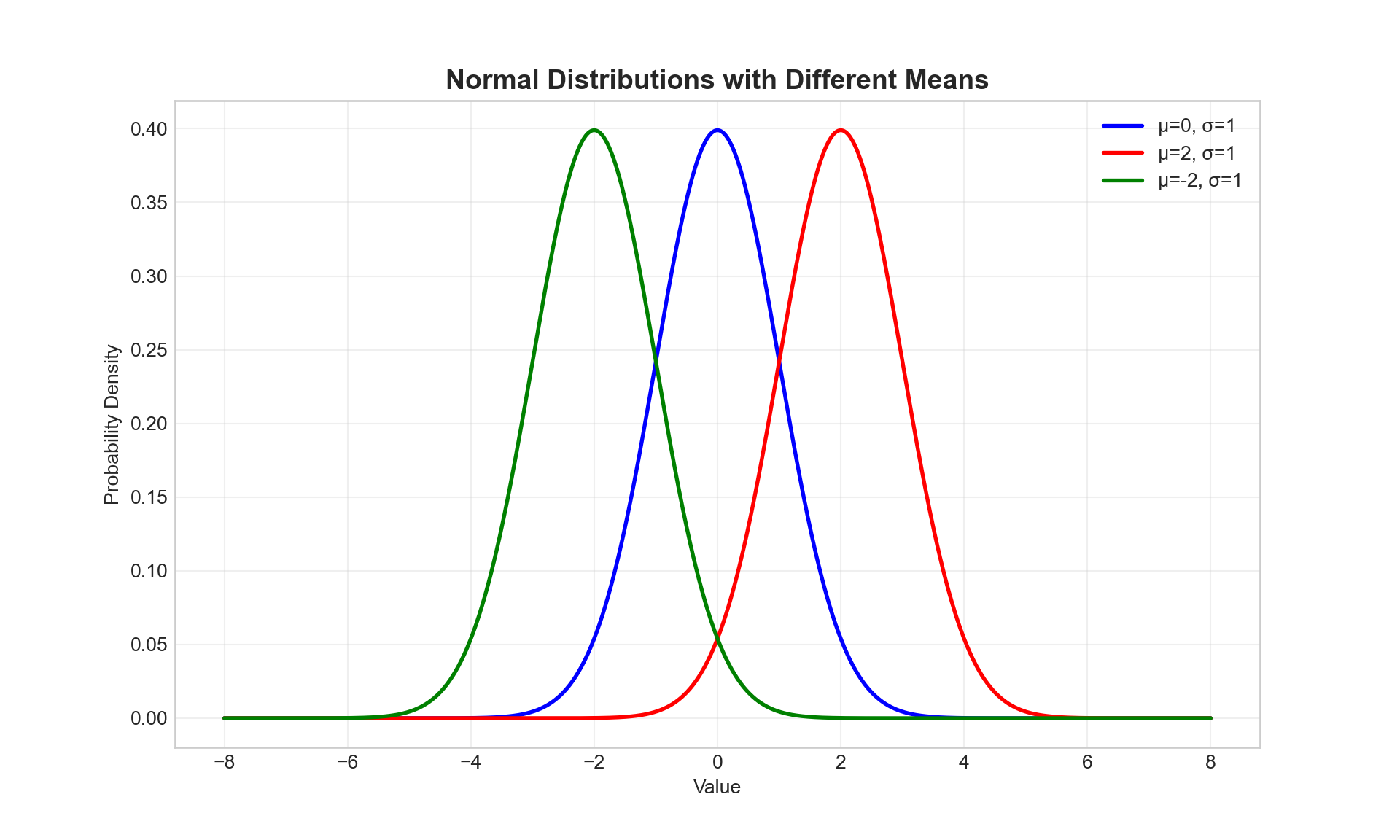

Effect of Standard Deviation

# Same mean, different standard deviations
x = np.linspace(-8, 8, 1000)

y1 = norm.pdf(x, loc=0, scale=0.5)  # μ=0, σ=0.5
y2 = norm.pdf(x, loc=0, scale=1)    # μ=0, σ=1
y3 = norm.pdf(x, loc=0, scale=2)    # μ=0, σ=2

plt.figure(figsize=(10, 6))
plt.plot(x, y1, 'b-', linewidth=2, label='μ=0, σ=0.5')
plt.plot(x, y2, 'r-', linewidth=2, label='μ=0, σ=1')
plt.plot(x, y3, 'g-', linewidth=2, label='μ=0, σ=2')

plt.title('Normal Distributions with Different Standard Deviations', fontsize=14, fontweight='bold')
plt.xlabel('Value')
plt.ylabel('Probability Density')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()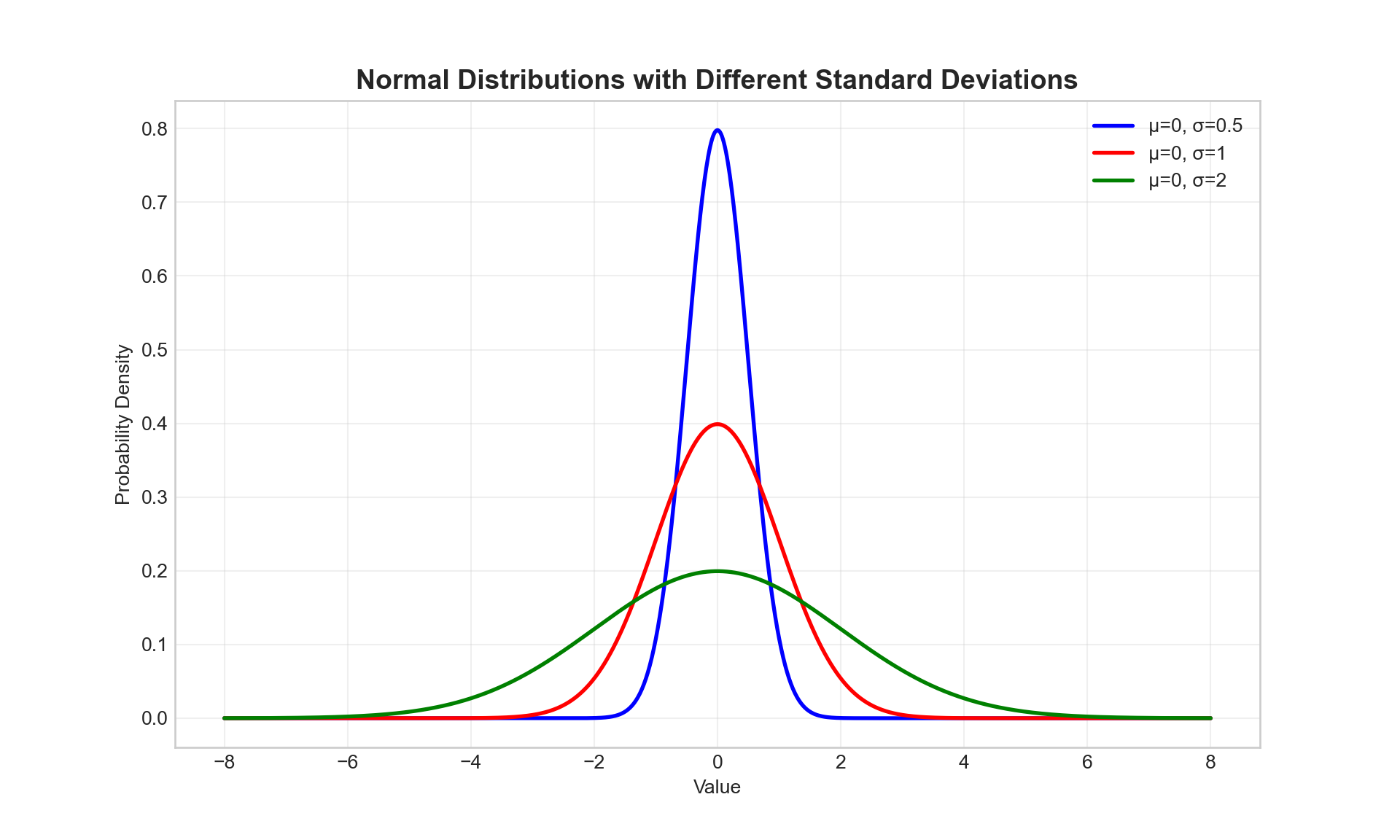

The Standard Normal Distribution

The standard normal distribution is a special case where μ = 0 and σ = 1.

# Standard normal distribution with empirical rule
x = np.linspace(-4, 4, 1000)
y = norm.pdf(x, 0, 1)

plt.figure(figsize=(10, 6))

# Fill areas for empirical rule
plt.fill_between(x, y, where=(x >= -1) & (x <= 1), alpha=0.3, color='green', label='68% (±1σ)')
plt.fill_between(x, y, where=(x >= -2) & (x <= 2), alpha=0.2, color='orange', label='95% (±2σ)')
plt.fill_between(x, y, where=(x >= -3) & (x <= 3), alpha=0.1, color='red', label='99.7% (±3σ)')

plt.plot(x, y, 'black', linewidth=2)
plt.axvline(0, color='black', linestyle='--', alpha=0.5)

plt.title('Standard Normal Distribution - Empirical Rule', fontsize=14, fontweight='bold')
plt.xlabel('Standard deviations from mean')
plt.ylabel('Probability Density')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()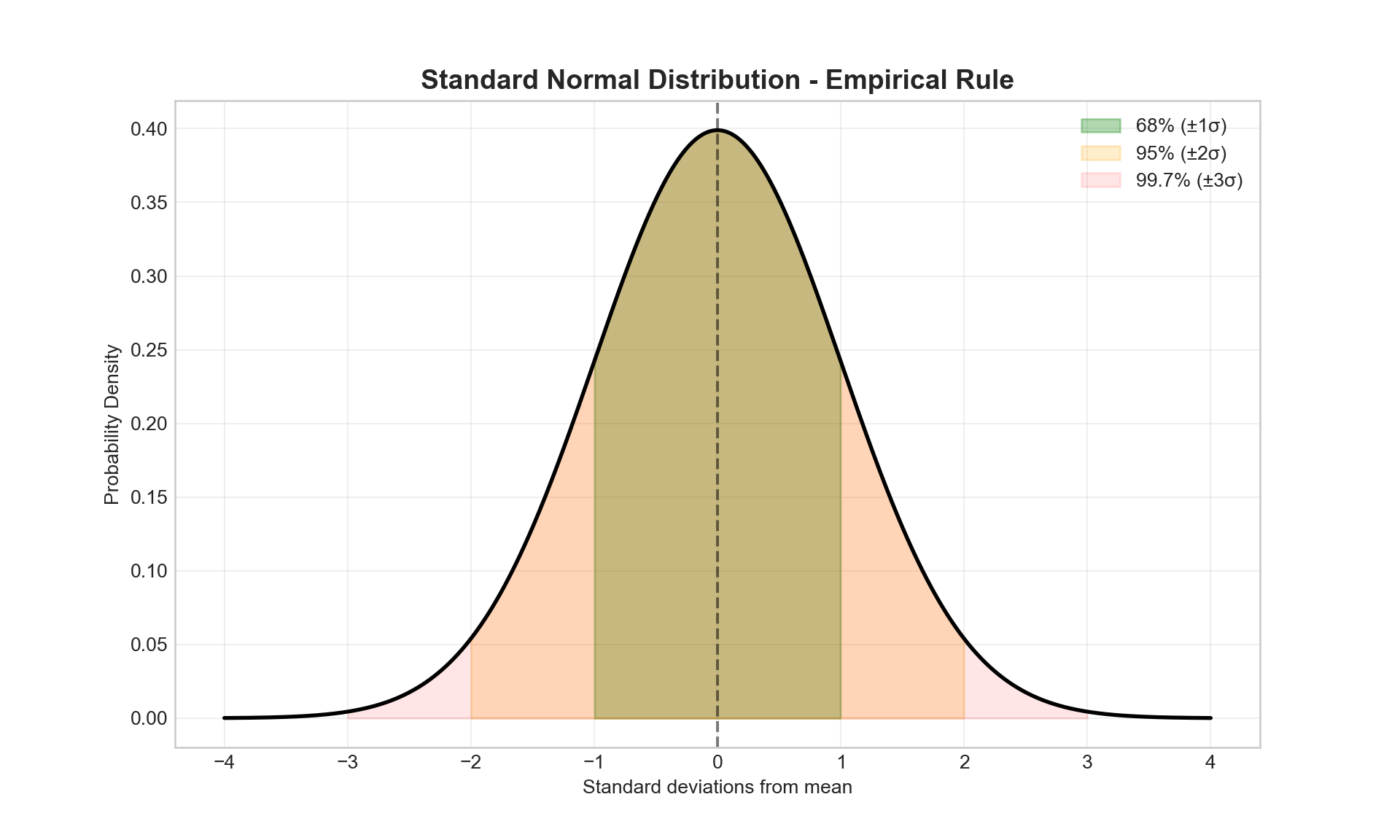

The Empirical Rule (68-95-99.7 Rule)

For any normal distribution:

• 68% of data falls within 1 standard deviation of the mean
• 95% of data falls within 2 standard deviations of the mean
  
• 99.7% of data falls within 3 standard deviations of the mean

# Let's verify this with actual calculations
print("Empirical Rule Verification:")

Empirical Rule Verification:

print(f"P(-1 ≤ Z ≤ 1) = {norm.cdf(1) - norm.cdf(-1):.1%}")

P(-1 ≤ Z ≤ 1) = 68.3%

print(f"P(-2 ≤ Z ≤ 2) = {norm.cdf(2) - norm.cdf(-2):.1%}")

P(-2 ≤ Z ≤ 2) = 95.4%

print(f"P(-3 ≤ Z ≤ 3) = {norm.cdf(3) - norm.cdf(-3):.1%}")

P(-3 ≤ Z ≤ 3) = 99.7%

68 - 95 - 99.7 Rule

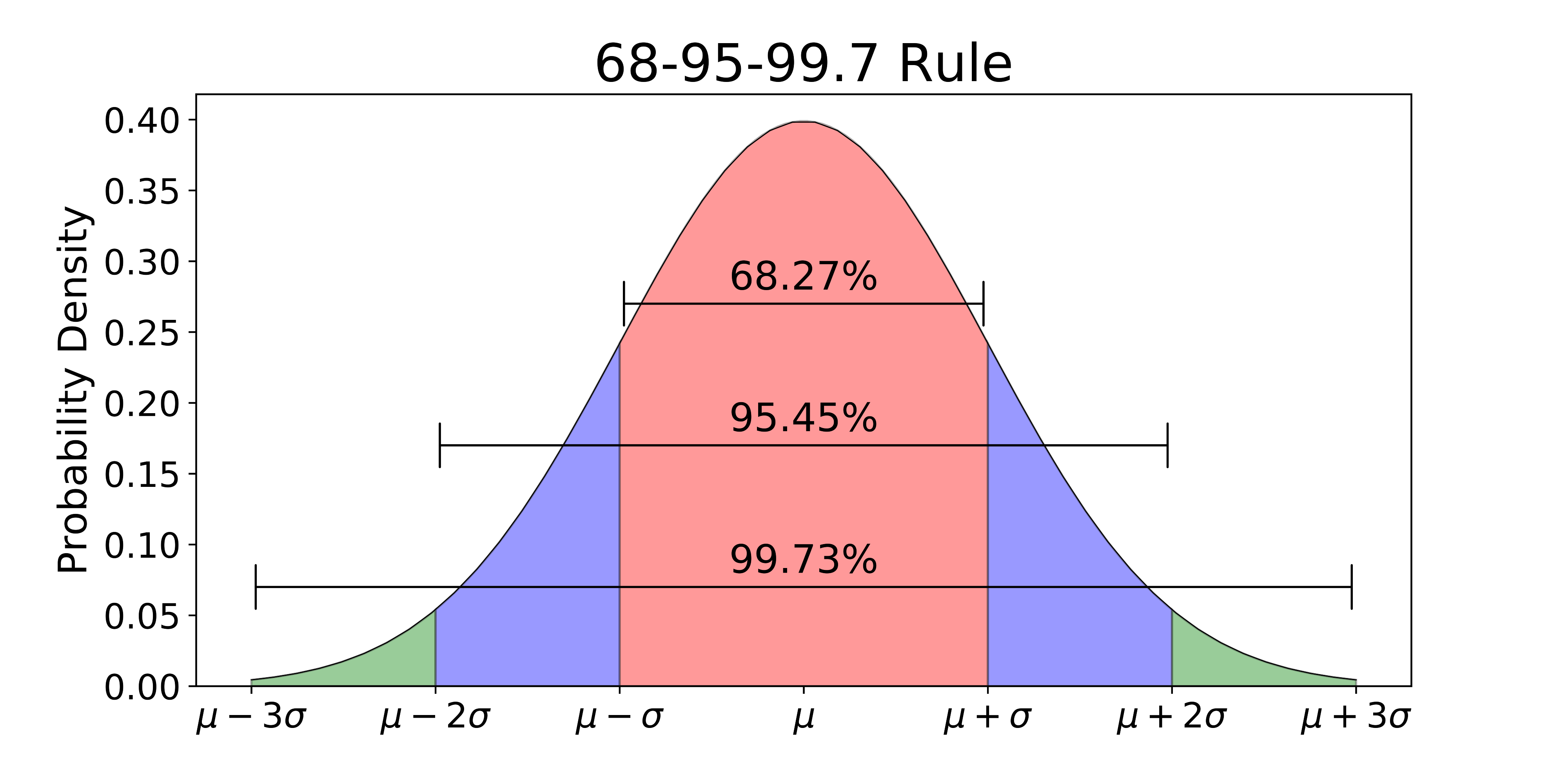
Real-World Example: Heights

Human heights often follow a normal distribution.

# Simulate height data (in cm)
np.random.seed(42)
male_heights = np.random.normal(175, 7, 1000)    # μ=175cm, σ=7cm
female_heights = np.random.normal(162, 6, 1000)  # μ=162cm, σ=6cm

plt.figure(figsize=(10, 6))
plt.hist(male_heights, bins=30, alpha=0.7, label='Male Heights', density=True)
plt.hist(female_heights, bins=30, alpha=0.7, label='Female Heights', density=True)

# Overlay theoretical curves
x_male = np.linspace(150, 200, 1000)
x_female = np.linspace(140, 185, 1000)
plt.plot(x_male, norm.pdf(x_male, 175, 7), 'b-', linewidth=2)
plt.plot(x_female, norm.pdf(x_female, 162, 6), 'orange', linewidth=2)

plt.title('Distribution of Heights', fontsize=14, fontweight='bold')
plt.xlabel('Height (cm)')
plt.ylabel('Density')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()

The Central Limit Theorem

The Central Limit Theorem (CLT) states:

“Regardless of the shape of the original population distribution, the distribution of sample means approaches a normal distribution as the sample size increases.”

Key points:

• Works for any population distribution (uniform, exponential, skewed, etc.)
• Sample size should be n ≥ 30 (rule of thumb)
• The mean of sample means equals the population mean: \(\mu_{\bar{x}} = \mu\)
• The standard deviation of sample means: \(\sigma_{\bar{x}} = \frac{\sigma}{\sqrt{n}}\)

Why is this important? - Allows us to make inferences about populations using sample data - Foundation for confidence intervals and hypothesis testing - Explains why many real-world phenomena follow normal distributions

CLT Demonstration: Uniform Distribution

Let’s start with a uniform distribution (definitely not normal!):

# Set up the demonstration
np.random.seed(42)
population = np.random.uniform(0, 10, 10000)  # Uniform distribution from 0 to 10

sample_sizes = [1, 5, 30, 100]
sample_means = {n: [] for n in sample_sizes}

# Generate sample means for different sample sizes
for n in sample_sizes:
    for _ in range(1000):
        sample = np.random.choice(population, n)
        sample_means[n].append(np.mean(sample))

# Create subplots
fig, axes = plt.subplots(2, 3, figsize=(12, 8))
fig.suptitle('Central Limit Theorem Demonstration', fontsize=16, fontweight='bold');

# Plot original population
axes[0, 0].hist(population, bins=30, alpha=0.7, color='red', density=True);
axes[0, 0].set_title('Original Population\n(Uniform Distribution)');
axes[0, 0].set_ylabel('Density');

# Plot sample means for different sample sizes
positions = [(0, 1), (0, 2), (1, 0), (1, 1)]
for i, n in enumerate(sample_sizes):
    row, col = positions[i];
    axes[row, col].hist(sample_means[n], bins=30, alpha=0.7, density=True);
    axes[row, col].set_title(f'Sample Means (n={n})');
    axes[row, col].set_ylabel('Density');
    
    # Overlay normal curve for larger sample sizes
    if n >= 30:
        x = np.linspace(min(sample_means[n]), max(sample_means[n]), 100);
        mu = np.mean(sample_means[n]);
        sigma = np.std(sample_means[n]);
        axes[row, col].plot(x, norm.pdf(x, mu, sigma), 'r-', linewidth=2)

(array([0.12637529, 0.093277  , 0.10230381, 0.08425019, 0.10230381,
       0.11734848, 0.10230381, 0.10531274, 0.10230381, 0.07823232,
       0.07823232, 0.10531274, 0.08725913, 0.11133061, 0.08425019,
       0.11734848, 0.10230381, 0.09026806, 0.11433955, 0.11133061,
       0.08725913, 0.07823232, 0.12035742, 0.08725913, 0.13239316,
       0.06017871, 0.10531274, 0.08124126, 0.12035742, 0.12035742]), array([5.97938835e-03, 3.38322841e-01, 6.70666294e-01, 1.00300975e+00,
       1.33535320e+00, 1.66769665e+00, 2.00004011e+00, 2.33238356e+00,
       2.66472701e+00, 2.99707046e+00, 3.32941392e+00, 3.66175737e+00,
       3.99410082e+00, 4.32644428e+00, 4.65878773e+00, 4.99113118e+00,
       5.32347463e+00, 5.65581809e+00, 5.98816154e+00, 6.32050499e+00,
       6.65284845e+00, 6.98519190e+00, 7.31753535e+00, 7.64987880e+00,
       7.98222226e+00, 8.31456571e+00, 8.64690916e+00, 8.97925262e+00,
       9.31159607e+00, 9.64393952e+00, 9.97628297e+00]), <BarContainer object of 30 artists>)
Text(0.5, 1.0, 'Sample Means (n=1)')
Text(0, 0.5, 'Density')
(array([0.00769475, 0.00769475, 0.0153895 , 0.01923688, 0.030779  ,
       0.08079488, 0.10387913, 0.13081076, 0.13850551, 0.16543713,
       0.21545301, 0.26931626, 0.28085839, 0.24623201, 0.31163739,
       0.27316364, 0.26162151, 0.24623201, 0.28470577, 0.15004763,
       0.15389501, 0.13850551, 0.09233701, 0.08848963, 0.061558  ,
       0.02693163, 0.01154213, 0.02308425, 0.00384738, 0.00769475]), array([1.14761917, 1.40753663, 1.66745409, 1.92737155, 2.18728902,
       2.44720648, 2.70712394, 2.9670414 , 3.22695886, 3.48687632,
       3.74679379, 4.00671125, 4.26662871, 4.52654617, 4.78646363,
       5.04638109, 5.30629856, 5.56621602, 5.82613348, 6.08605094,
       6.3459684 , 6.60588587, 6.86580333, 7.12572079, 7.38563825,
       7.64555571, 7.90547317, 8.16539064, 8.4253081 , 8.68522556,
       8.94514302]), <BarContainer object of 30 artists>)
Text(0.5, 1.0, 'Sample Means (n=5)')
Text(0, 0.5, 'Density')
(array([0.05933713, 0.01977904, 0.02966857, 0.03955809, 0.0890057 ,
       0.14834283, 0.16812187, 0.27690661, 0.33624374, 0.42524943,
       0.38569135, 0.70215604, 0.80105126, 0.89005695, 0.69226652,
       0.86038839, 0.78127221, 0.64281891, 0.60326082, 0.39558087,
       0.46480752, 0.35602278, 0.25712756, 0.1384533 , 0.09889522,
       0.11867426, 0.00988952, 0.00988952, 0.04944761, 0.03955809]), array([3.46094648, 3.56206361, 3.66318073, 3.76429786, 3.86541498,
       3.96653211, 4.06764923, 4.16876636, 4.26988348, 4.37100061,
       4.47211773, 4.57323486, 4.67435198, 4.77546911, 4.87658623,
       4.97770336, 5.07882048, 5.17993761, 5.28105473, 5.38217186,
       5.48328898, 5.58440611, 5.68552323, 5.78664035, 5.88775748,
       5.9888746 , 6.08999173, 6.19110885, 6.29222598, 6.3933431 ,
       6.49446023]), <BarContainer object of 30 artists>)
Text(0.5, 1.0, 'Sample Means (n=30)')
Text(0, 0.5, 'Density')
[<matplotlib.lines.Line2D object at 0x000000006E699A30>]
(array([0.11818307, 0.08441648, 0.11818307, 0.11818307, 0.33766592,
       0.35454921, 0.4051991 , 0.60779865, 0.64156524, 0.84416479,
       1.09741422, 1.02988104, 1.16494741, 1.30001377, 1.62079639,
       1.31689707, 1.33378037, 1.09741422, 0.91169797, 0.57403206,
       0.52338217, 0.4051991 , 0.4051991 , 0.15194966, 0.10129977,
       0.05064989, 0.08441648, 0.05064989, 0.        , 0.03376659]), array([4.12606403, 4.18529417, 4.24452431, 4.30375445, 4.36298459,
       4.42221474, 4.48144488, 4.54067502, 4.59990516, 4.6591353 ,
       4.71836544, 4.77759559, 4.83682573, 4.89605587, 4.95528601,
       5.01451615, 5.07374629, 5.13297644, 5.19220658, 5.25143672,
       5.31066686, 5.369897  , 5.42912714, 5.48835728, 5.54758743,
       5.60681757, 5.66604771, 5.72527785, 5.78450799, 5.84373813,
       5.90296828]), <BarContainer object of 30 artists>)
Text(0.5, 1.0, 'Sample Means (n=100)')
Text(0, 0.5, 'Density')
[<matplotlib.lines.Line2D object at 0x000000006C5EB980>]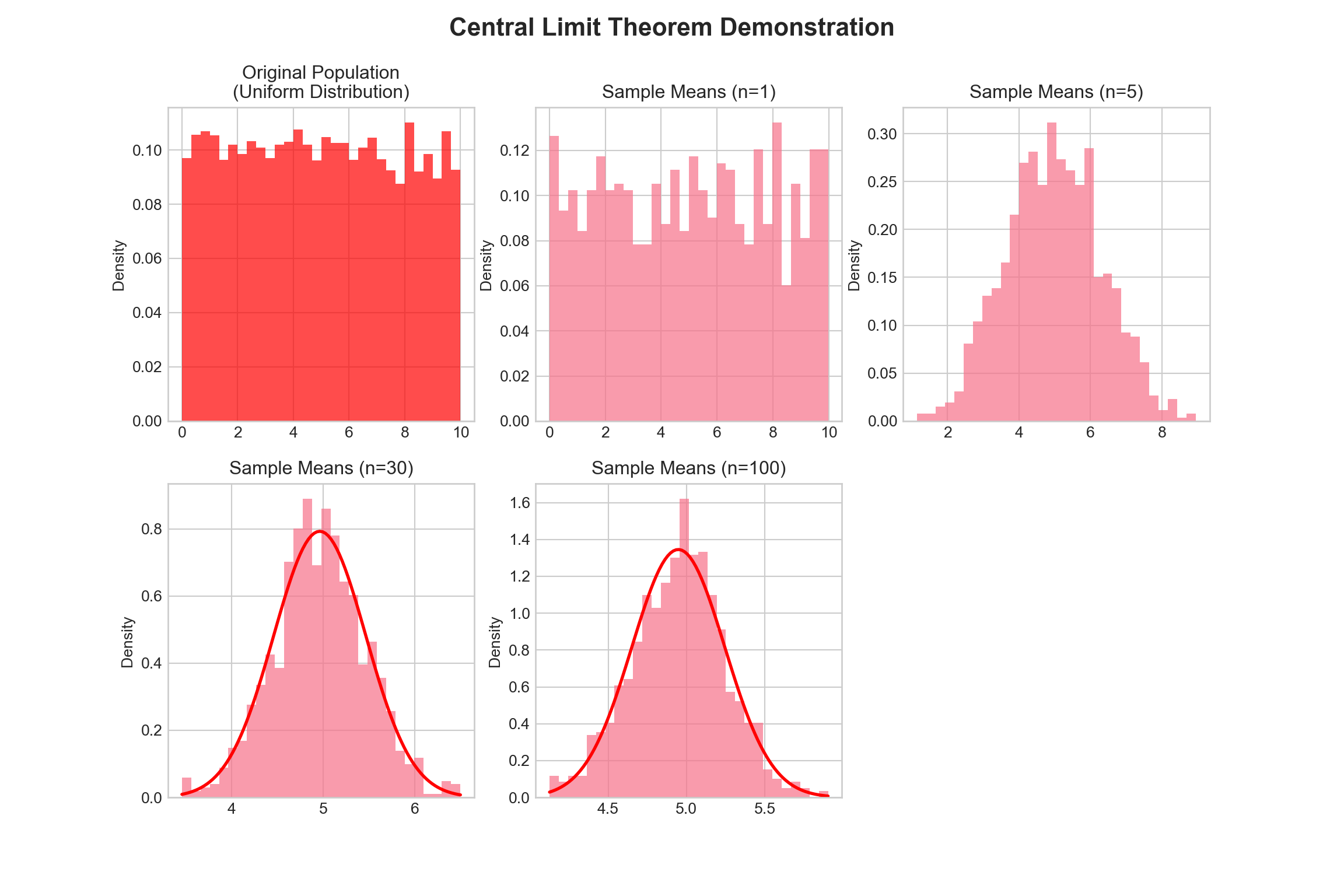

# Remove empty subplot
axes[1, 2].remove();

plt.tight_layout()
plt.show()

Summary

• Normal distributions are fundamental to statistics and appear everywhere in nature
• The empirical rule helps us understand what ‘normal’ variation looks like
  
• The Central Limit Theorem is one of the most important theorems in statistics
• CLT allows us to use normal distribution tools even when our data isn’t normal
• Sample size matters: larger samples give better normal approximations
• These concepts are essential for confidence intervals, hypothesis testing, and quality control

Next steps: Practice with real datasets, explore confidence intervals, and learn hypothesis testing!