PassengerId Survived Pclass ... Fare Cabin Embarked
0 1 0 3 ... 7.2500 NaN S
1 2 1 1 ... 71.2833 C85 C
2 3 1 3 ... 7.9250 NaN S
3 4 1 1 ... 53.1000 C123 S
4 5 0 3 ... 8.0500 NaN S
[5 rows x 12 columns]Machine Learning
Wednesday 16th July 2025
Jupyterlab
Relevant code and data will be provided in a Jupyterlab instance available at:
https://tinyurl.com/asdanpython

Motivation
Why Machine Learning?
- Machine learning allows us to make data-driven decisions and predictions.
- It can handle large and complex datasets that traditional methods struggle with.
- Machine learning models can improve over time with more data.
- It is widely used in various industries such as healthcare, finance, and technology.
Real-World Applications
- Healthcare: Predicting disease outbreaks, personalized treatment plans.
- Finance: Fraud detection, stock market prediction.
- Technology: Image and speech recognition, recommendation systems.
- Retail: Customer segmentation, inventory management.
Benefits of Machine Learning
- Efficiency: Automates repetitive tasks and processes large amounts of data quickly.
- Accuracy: Provides more accurate predictions and insights compared to traditional methods.
- Scalability: Can be applied to various domains and scaled to handle increasing data volumes.
- Adaptability: Models can adapt to new data and improve over time.
Types of Machine Learning
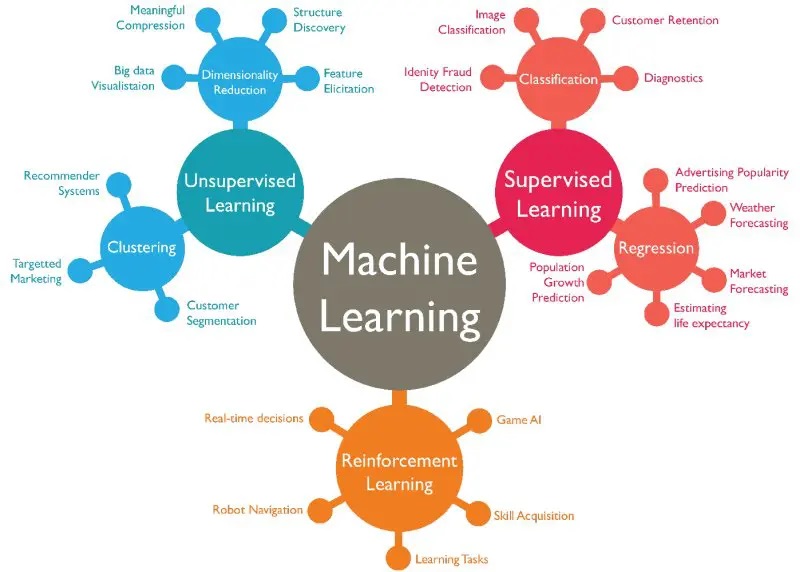
Part 2: Theory
Terminology - Dataframe
This is a commonly used data structure in data science. It is tabular data structure with some constraints that make it simpler to work with.
Every row is an observation in the data.
Every column is a variable in the data.
A variable will have a specific data type e.g. number, text, date.
We will make frequent use of pandas dataframes.
scikit-learn
We will be using models from the scikit-learn package in this lecture.
There is extensive documentation with examples available at:
https://scikit-learn.org/stable/supervised_learning.html

Difference Between Classification and Regression
Classification
- Predicts categorical labels.
- Example: Predicting if an email is spam or not spam.
Regression
- Predicts continuous values.
- Example: Predicting the price of a house.
Naming Conventions
- Feature = predictor variable = independent variable
- Target variable = dependent variable = response variable
Introduction to k-NN
- k-Nearest Neighbors (k-NN) is a classification method.
- Suitable for binary or multi-class classification.
- Classifies a new data point based on the majority class of its k nearest neighbors.
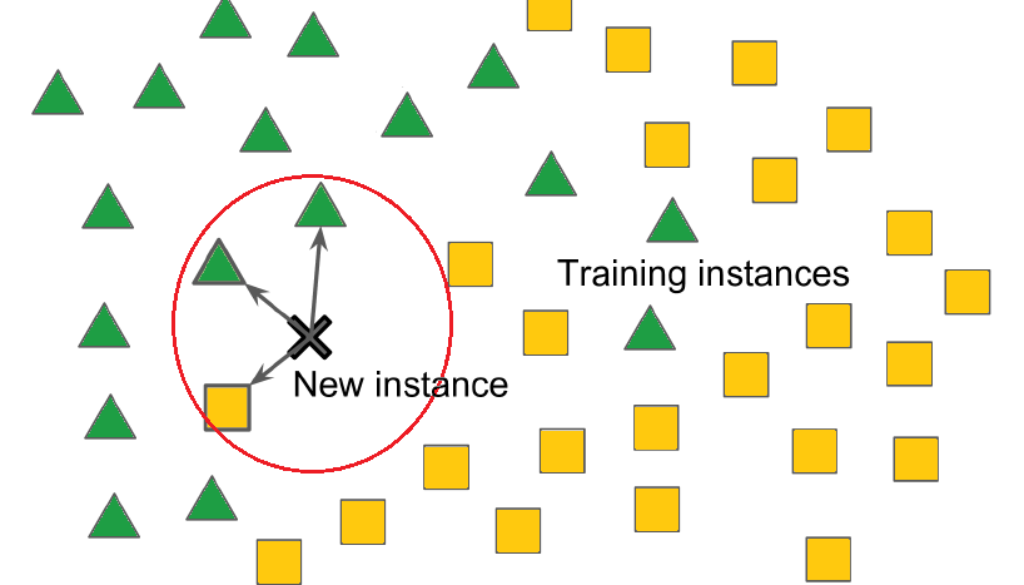
source: https://mlarchive.com/
Binary Classification Example: Titanic Dataset
In this example, we will use the Titanic dataset to predict whether a passenger survived or not.
The target variable is survived it is a binary value, so the model will predict 0 or 1.
head() and tail() function
We can view the first few rows of a pandas dataframe with the head() function
Similarly we can view end of a dataframe with tail()
describe() function
We can get summary statistics of each column with the describe() function.
PassengerId Survived Pclass ... SibSp Parch Fare
count 891.000000 891.000000 891.000000 ... 891.000000 891.000000 891.000000
mean 446.000000 0.383838 2.308642 ... 0.523008 0.381594 32.204208
std 257.353842 0.486592 0.836071 ... 1.102743 0.806057 49.693429
min 1.000000 0.000000 1.000000 ... 0.000000 0.000000 0.000000
25% 223.500000 0.000000 2.000000 ... 0.000000 0.000000 7.910400
50% 446.000000 0.000000 3.000000 ... 0.000000 0.000000 14.454200
75% 668.500000 1.000000 3.000000 ... 1.000000 0.000000 31.000000
max 891.000000 1.000000 3.000000 ... 8.000000 6.000000 512.329200
[8 rows x 7 columns]train_test_split() function
# Import the module
from sklearn.model_selection import train_test_split
X = titanic.drop("Survived", axis=1).values
y = titanic["Survived"].values
# Split into training and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42, stratify=y)
print(y_train.sum()/len(y_train))0.383426966292134850.38547486033519550.3838383838383838pandas cheat sheets
You can download a pdf of the pandas cheat sheet from their docs website at:
https://pandas.pydata.org/Pandas_Cheat_Sheet.pdf



Mathematics of \(R^n\) Vectors
- Introduce the concept of vectors in \(R^n\).
- Explain vector operations and their significance in machine learning.
Euclidean Distance
To calculate the Euclidean distance between two points \((x_1, y_1)\) and \((x_2, y_2)\), we use the formula:
\[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
For the points \((2, 3)\) and \((8, 5)\), the Euclidean distance is calculated as follows:
\[ d = \sqrt{(8 - 2)^2 + (5 - 3)^2} = \sqrt{6^2 + 2^2} = \sqrt{36 + 4} = \sqrt{40} = 2\sqrt{10} \]
Example in \(\mathbb{R}^3\)
To calculate the Euclidean distance between two points in \(\mathbb{R}^3\), we use the formula:
\[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2} \]
For the points \((1, 2, 3)\) and \((4, 5, 6)\), the Euclidean distance is calculated as follows:
\[ d = \sqrt{(4 - 1)^2 + (5 - 2)^2 + (6 - 3)^2} = \sqrt{3^2 + 3^2 + 3^2} = \sqrt{9 + 9 + 9} = \sqrt{27} = 3\sqrt{3} \]
General Formula in \(\mathbb{R}^n\)
The general formula for calculating the Euclidean distance between two points in \(\mathbf{X}_1\) and \(\mathbf{X}_2\)\(\mathbb{R}^n\)
where
\[ \mathbf{X}_1 = \{x_{1_1}, x_{2_1}, x_{3_1}, \ldots, x_{n_1}\} \]
and
\[ \mathbf{X}_2 = \{x_{1_2}, x_{2_2}, x_{3_2}, \ldots, x_{n_2}\} \]
\[ d = \sqrt{\sum_{i=1}^{n} (x_{i_2} - x_{i_1})^2} \]
where \(x_{i1}\) and \(x_{i2}\) are the coordinates of the two points in the \(i\)-th dimension.
Part 3: Practice
Code Examples in Python
- Provide an introduction to Python libraries such as pandas and scikit-learn.
- Show how to load and preprocess data using pandas.
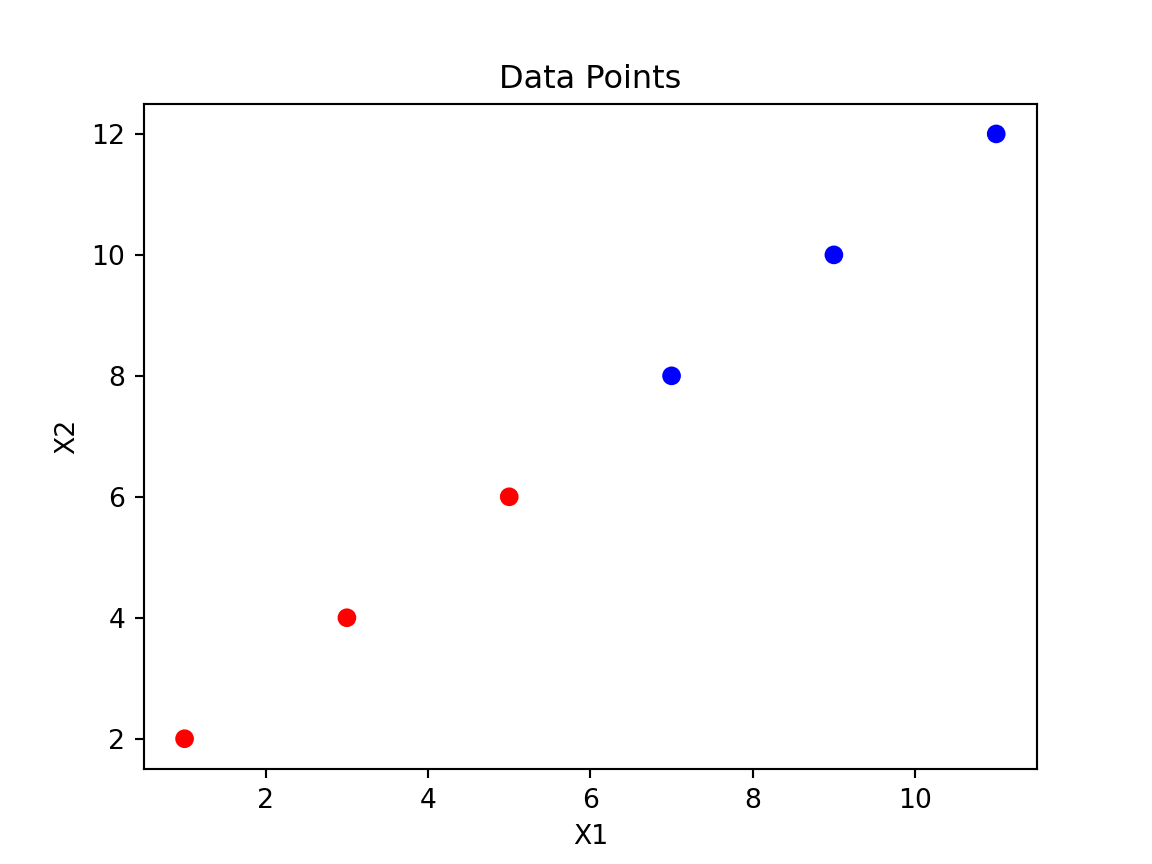
Creating Data Points in Python
import pandas as pd
# Create a DataFrame with six varied data points
data = {
'X1': [1, 3, 5, 7, 9, 11],
'X2': [2, 4, 6, 8, 10, 12],
'y': ['red', 'red', 'red', 'blue', 'blue', 'blue']
}
df = pd.DataFrame(data)
# Map 'red' to 0 and 'blue' to 1
color_map = {'red': 0, 'blue': 1}
df['y'] = df['y'].map(color_map)| X1 | X2 | y |
|---|---|---|
| 1 | 2 | 0 |
| 3 | 4 | 0 |
| 5 | 6 | 0 |
| 7 | 8 | 1 |
| 9 | 10 | 1 |
| 11 | 12 | 1 |
Explanation of Variables
- X1 and X2 are independent variables.
- y is the target variable, which is binary (0 for red, 1 for blue).
Plotting Data Points using Matplotlib
scikit-learn Syntax
scikit-learn Syntax with Train Test Split
from scikit-learn.module import Model
from sklearn.model_selection import train_test_split
# Create an instance of the model
model = Model()
# Split the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=prop)
# Fit the model to the data
model.fit(X_train, y_train)
# Make predictions on new data
predictions = model.predict(X_test)
# Print the accuracy
print(model.score(X_test, y_test))k-NN Example
from sklearn.neighbors import KNeighborsClassifier
import numpy as np
# Prepare the data
X = df[['X1', 'X2']].values
y = df['y'].values
# Create and train the k-NN classifier
knn = KNeighborsClassifier(n_neighbors=3)
knn.fit(X, y)KNeighborsClassifier(n_neighbors=3)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
KNeighborsClassifier(n_neighbors=3)
k-NN Example Output
KNeighborsClassifier(n_neighbors=3)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
KNeighborsClassifier(n_neighbors=3)
The new point [[8 8]] is classified as blue.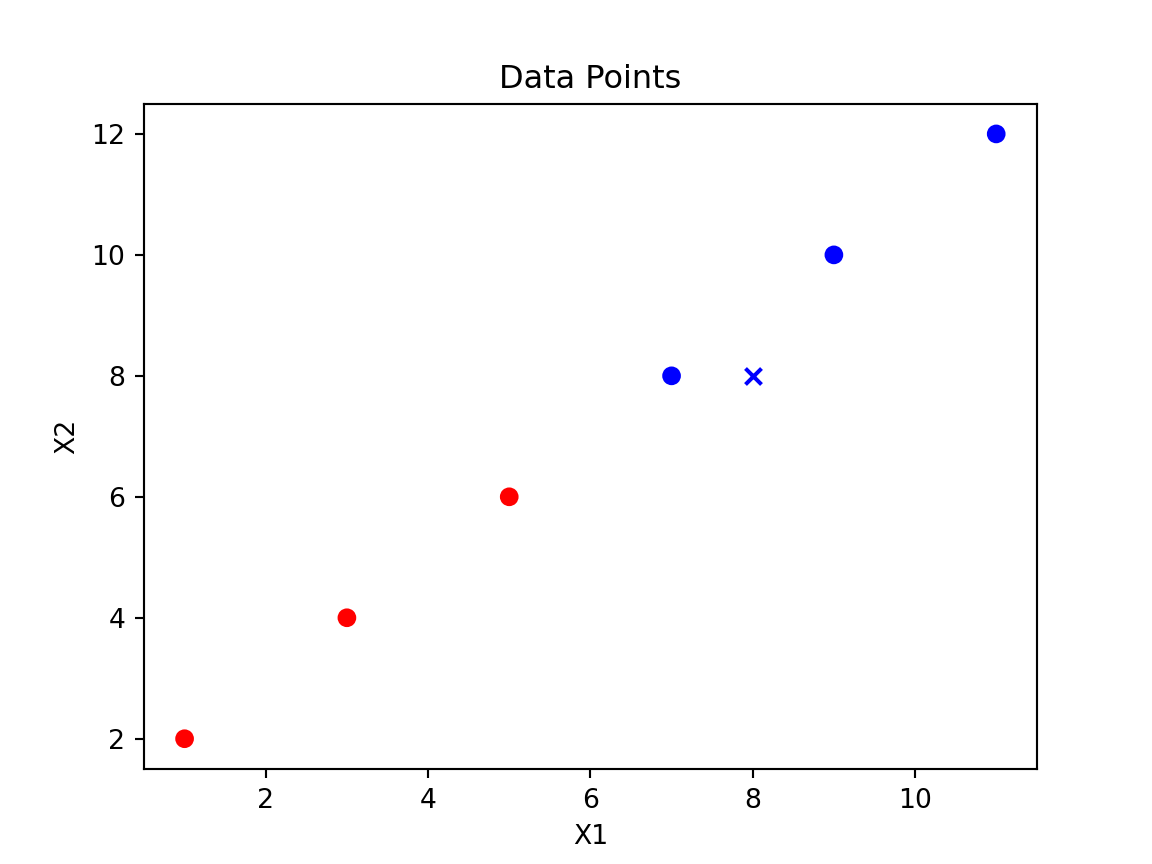
k-NN Example with Iris Data (Two Variables)
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
import numpy as np
import matplotlib.pyplot as plt
# Load the iris dataset
iris = load_iris()
X = iris.data[:, :2] # Use only the first two features
y = iris.target
# Split the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# Plot all points
plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap='viridis', edgecolor='k', s=50)
plt.title('All Points')
plt.xlabel('Sepal Length')
plt.ylabel('Sepal Width')
# Plot train and test data separately
plt.subplot(1, 2, 2)
plt.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap='viridis', edgecolor='k', s=50, label='Train')
plt.scatter(X_test[:, 0], X_test[:, 1], c=y_test, cmap='viridis', edgecolor='k', s=50, label='Test', marker='x')
plt.title('Train and Test Data')
plt.xlabel('Sepal Length')
plt.ylabel('Sepal Width')
plt.legend()
plt.show()# Create and train the k-NN classifier
knn = KNeighborsClassifier(n_neighbors=3)
knn.fit(X_train, y_train)KNeighborsClassifier(n_neighbors=3)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
KNeighborsClassifier(n_neighbors=3)
k-NN Example with Iris Data (Two Variables) Output
KNeighborsClassifier(n_neighbors=3)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
KNeighborsClassifier(n_neighbors=3)
Correct predictions: 34 out of 45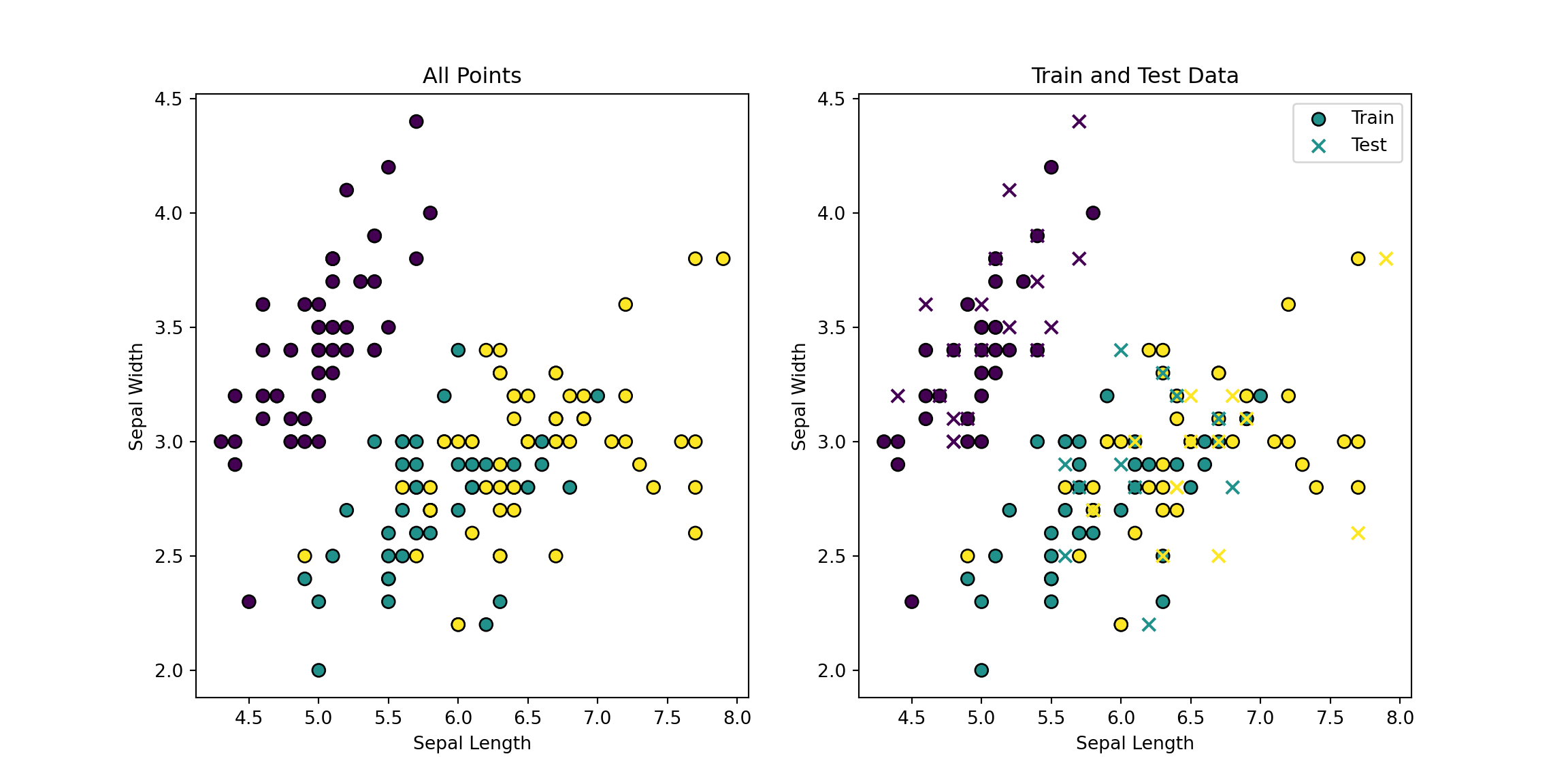
k-NN Example with Iris Data (All Variables)
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
import numpy as np
# Load the iris dataset
iris = load_iris()
X = iris.data # Use all four features
y = iris.target
# Split the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# Create and train the k-NN classifier
knn = KNeighborsClassifier(n_neighbors=3)
knn.fit(X_train, y_train)KNeighborsClassifier(n_neighbors=3)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
KNeighborsClassifier(n_neighbors=3)
k-NN Example with Iris Data (All Variables) Output
KNeighborsClassifier(n_neighbors=3)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
KNeighborsClassifier(n_neighbors=3)
Correct predictions: 45 out of 45Logistic Regression
- Logistic regression is a classification algorithm.
- It is used for binary classification.
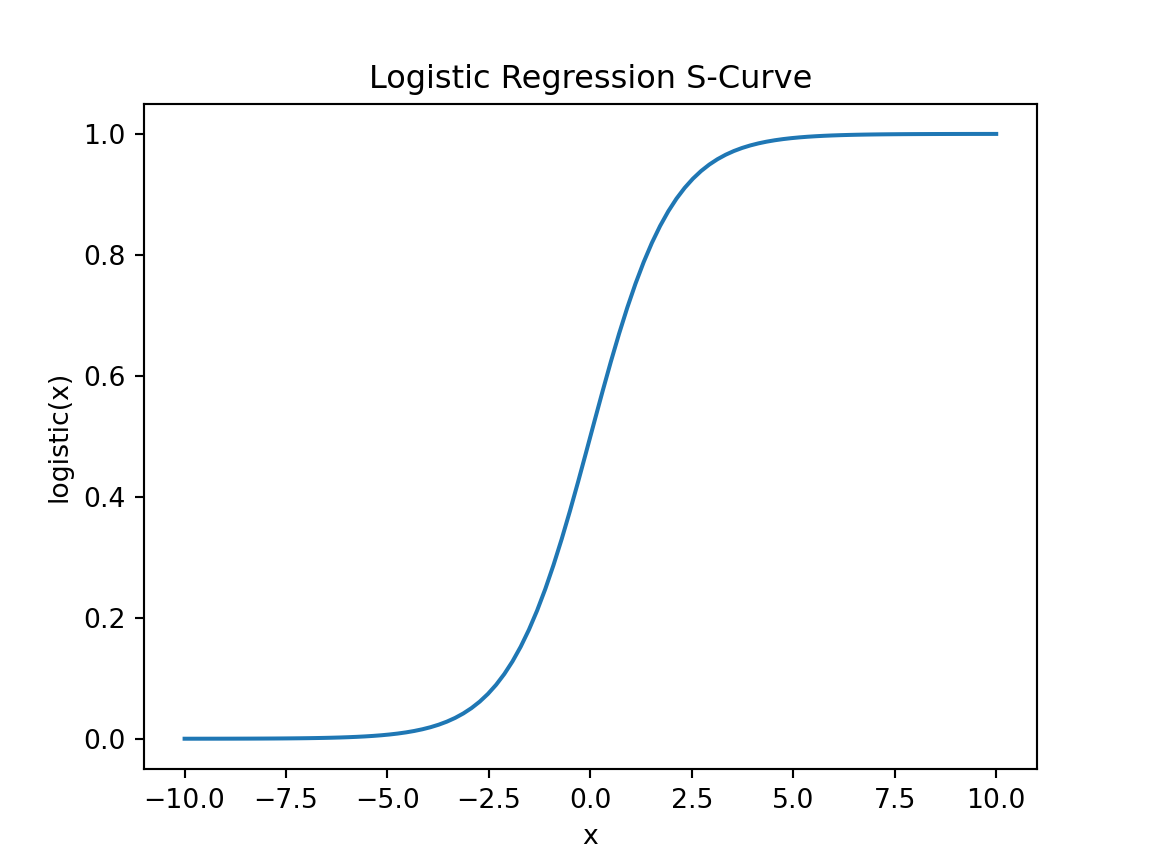
- The logistic function (S-curve) maps any real-valued number into the range [0, 1].
\[\frac{1}{1 + e^{-x}}\]
Logistic Regression S-Curve
Logistic Regression Example
from sklearn.linear_model import LogisticRegression
import numpy as np
# Prepare the data
X = df[['X1', 'X2']].values
y = df['y'].values
# Create and train the logistic regression model
log_reg = LogisticRegression()
log_reg.fit(X, y)
# Predict the class of a new point
new_point = np.array([[6, 7]])
predicted_class = log_reg.predict(new_point)
predicted_prob = log_reg.predict_proba(new_point)
predicted_color = 'red' if predicted_class == 0 else 'blue'
print(f'The new point {new_point} is classified as {predicted_color} with probability {predicted_prob}.')Logistic Regression Example Output
LogisticRegression()In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
LogisticRegression()
The new point [[6 7]] is classified as blue with probability [[0.4999958 0.5000042]].Dimensionality Reduction
Introduction to Dimensionality Reduction
- Dimensionality reduction is a technique used to reduce the number of features in a dataset.
- It helps in visualizing high-dimensional data and reducing computational complexity.
- Common dimensionality reduction techniques include PCA, t-SNE, and LDA.
Principal Component Analysis (PCA)
- PCA is a linear dimensionality reduction technique that projects the data onto a lower-dimensional space.
- It identifies the directions (principal components) that maximize the variance in the data.
- PCA is widely used for data visualization and noise reduction.
PCA Example
Code
from sklearn.decomposition import PCA
import numpy as np
import matplotlib.pyplot as plt
# Generate some sample data
X = np.random.rand(100, 5)
# Create and train the PCA model
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)
# Plot the PCA-transformed data
plt.scatter(X_pca[:, 0], X_pca[:, 1])
plt.title('PCA Example')
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.show()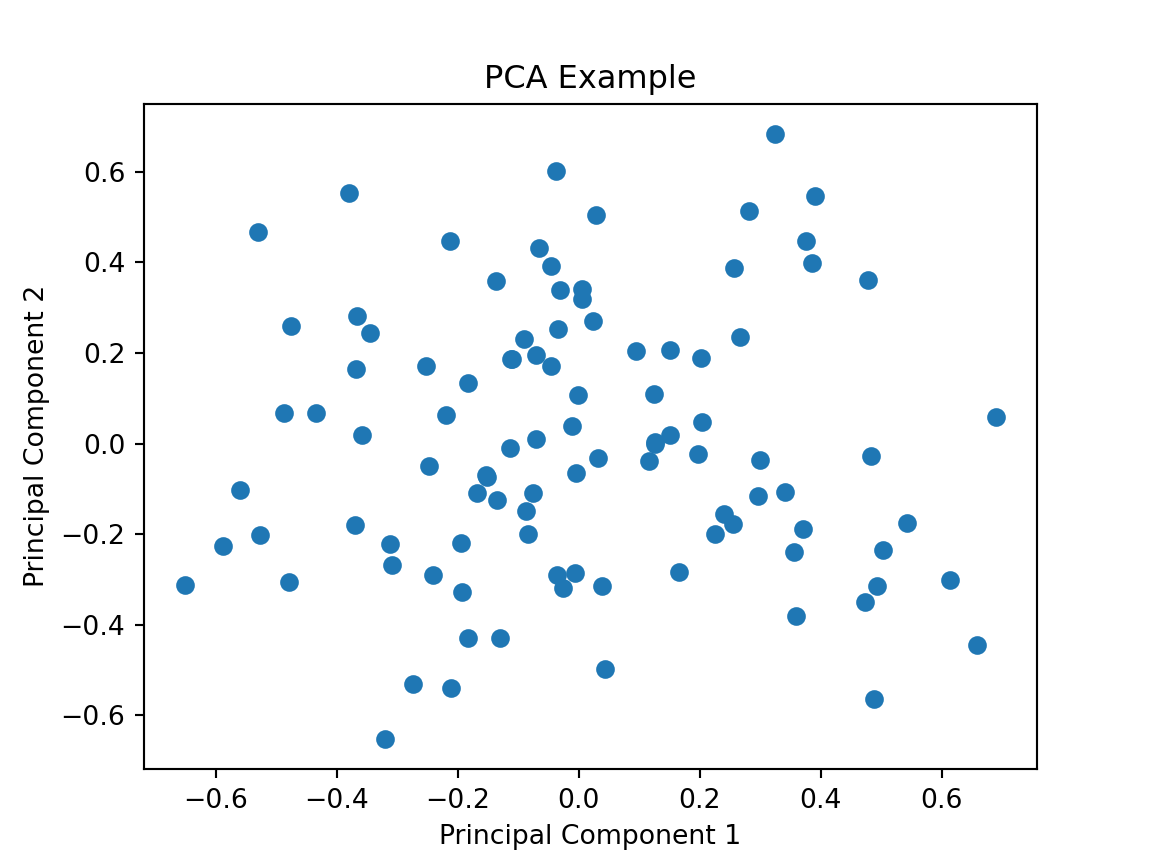
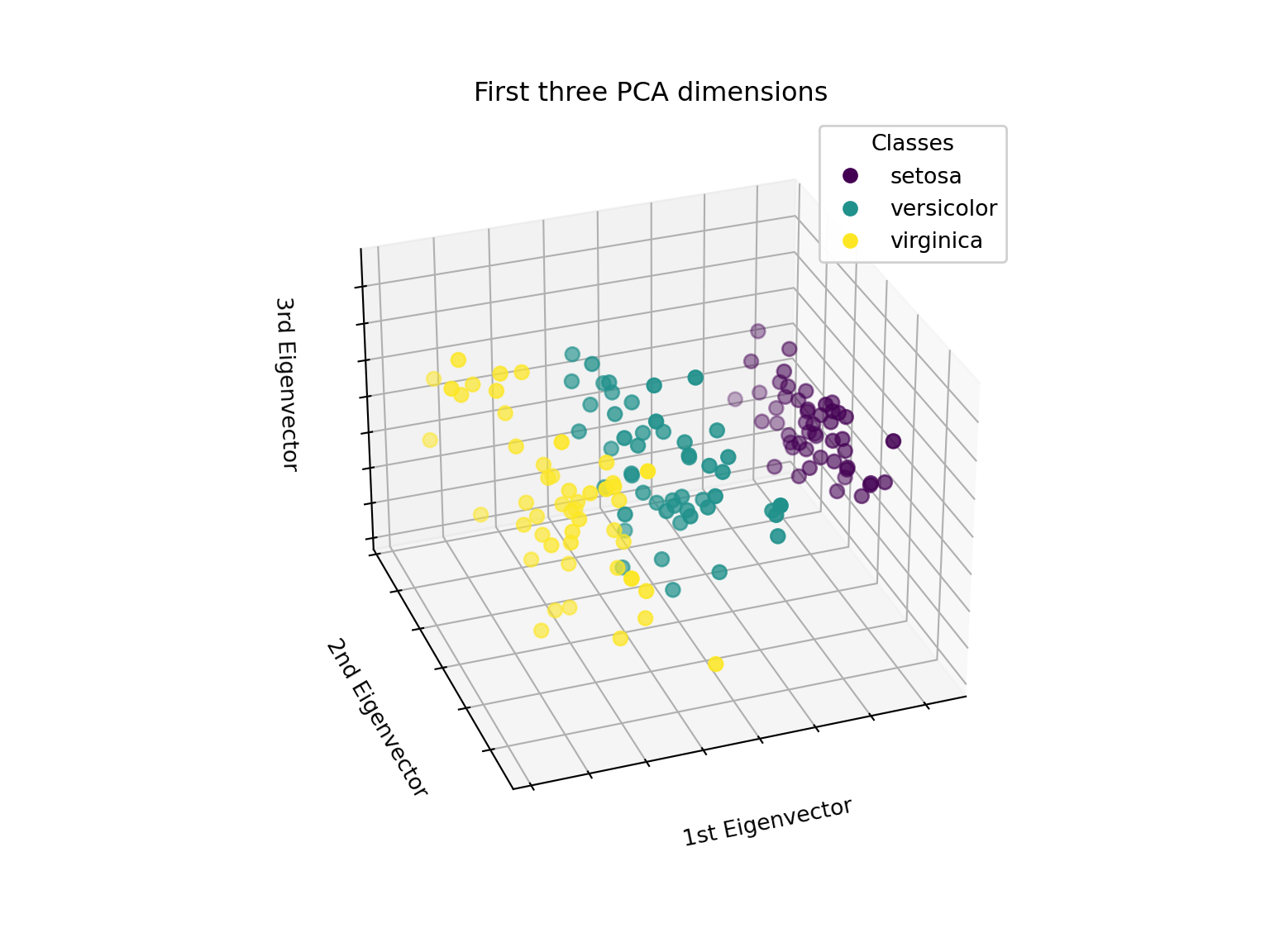
Scikit - Learn Iris Example
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause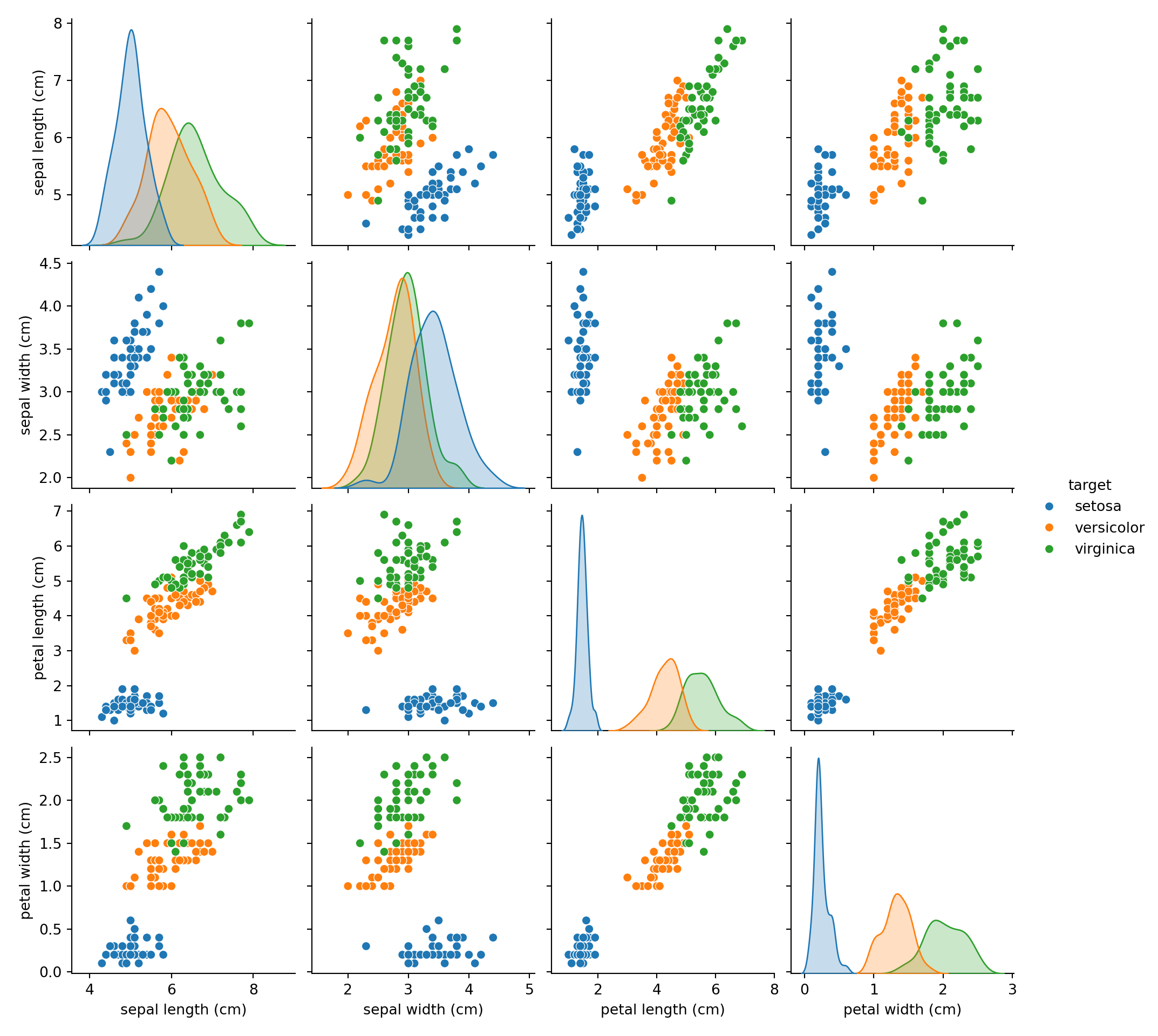
Scikit - Learn Iris Example cont

ASDAN July 2025